Archimedes and pi

In this post we take a look at Archimedes' approximation of the value of pi.  I'll try to make things as simple as I possibly can, but no simpler.

Here is the fundamental idea.  We will approximate the distance around a circle, called its circumference, by the distance around a regular polygon that just fits inside the circle, called its perimeter.  The points or vertices of the polygon will lie on the circle.

                                                 

It doesn't actually matter what kind of a polygon it is (i.e. how many sides there are), but it has to be regular, with sides all of the same length.  

For an inscribed polygon, the perimeter will be smaller than the circumference of the circle.

But the trick is, there is a way to compute the new perimeter for a polygon with twice the number of sides, 2n, given the original perimeter for n sides.  

Let's look at that what that means physically.  Actually, I'm going to show below just a small arc of the circle.  One side of our initial polygon will be colored red, and the chord it makes is the red line in the figure below.  The white area shows that it doesn't track very closely with the circle, and its length will be smaller than the length of this arc of the circle.

But then, when we double the number of sides, we get a polygon of 2n sides, and its perimeter follows the two blue lines.  This is clearly more like the circumference, there is less white space.  One side has become 2.

Double the number of sides again, to 4n.  The result is the magenta perimeter.  I hope you can see that as the number of sides gets larger, the perimeter of the polygon becomes a better and better approximation to the circumference of the circle.

This method is great, if you can find a way to express the new perimeter in terms of the old one each time. This is called the method of exhaustion and it was probably invented by a Greek mathematician named Eudoxus who lived before Archimedes.

To make things easier, we will only compute the lower limit.  That is, we will use inscribed polygons and compute their perimeters as we double the number of sides again and again.  

Python will do the actual computation.  Archimedes has this estimate in the end as 3-10/71 or about 3.140845.   Let's see how we compare.

Remember that pi is the ratio of the circumference of a circle, C, to its diameter.  If we use a circle whose diameter is equal to 1, then the circumference C will be equal to pi.  

The procedure we follow here is to inscribe a hexagon into a circle of diameter 1, and then calculate the length of the perimeter of the hexagon.  We do this because a hexagon's perimeter is particularly easy to find.

We will then derive a simple method to calculate the length of the perimeter after the number of sides is doubled (to give a 12-sided polygon).  This method will be applied repeatedly.  Archimedes reached 96 sides.  That is 4 doublings (6 - 12 - 24 - 48 - 96).

What he achieved is not just an estimate for the value of pi, it is an algorithm to compute the value of pi to any desired accuracy.

Begin with the hexagon.  A hexagon can be viewed as a group of six equilateral triangles.  Since the diameter of the circle will be 1, we choose the length of each triangle's side as 1/2.  This matches the diameter, made from two sides, and it results in a total perimeter of 6 times 1/2 or just 3.  

3 is our first lower bound for pi.

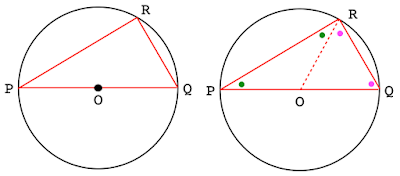
I introduced the side length of 1/2 above in order to see, even before we really get started, what the perimeter of the hexagon is and give a first estimate for the value of pi.  I must ask you to set that value aside for a minute.

We will need two ratios of sides in a right triangle, and it will make the math slightly easier if we scale the next equilateral triangle up to have a side length of 2 (we'll scale it back later, all we need are the ratios).  

Obtain a right triangle by cutting an equilateral triangle of side length 2 in half, so the base of the halved triangle is 1.  Pythagoras gives us the other side as the square root of 3, since 1^2 + 3 = 2^2.

Since the original triangle was equilateral, with angles of 60 degrees each, the halved triangle has one angle of 30 degrees.  Archimedes would call that measure one-third of a right angle, and the essential ratios for him would be 2 to 1 (hypotenuse to short side), and the square root of 3 to 1.

We have the angle that we're going to start with, 30 degrees, and we have two essential ratios.

The next graphic is a proof without words of Thales' famous circle theorem:  any angle inscribed in a semicircle is a right angle.  Since PQ is a diameter, the angle PRQ is a right angle.  

Proof.  the two smaller triangles formed by the radius OR are both isosceles, so by Euclid I.5 they have equal base angles.  Since the total of all the angles in a triangle is equal to two right angles and angle PRQ is one-half that, the result follows.

We're going to choose the angle P to have the particular value of 30 degrees.  Then the complementary angle Q is 60 degrees, and RQ can be viewed as one side of an inscribed hexagon.  (We won't prove it, but the peripheral angle P is one-half the measure of the central angle ROQ which cuts off the same arc of the circle).  That makes ROQ equilateral.

The ratios that we had above will apply, because P is a 30 degree angle in a right triangle.  So the ratio of PQ to RQ is 2, and the ratio of PR to RQ is the square root of 3.

We said that we will inscribe a hexagon into circle.  I don't actually have a picture of that, but I do have a picture of an octagon, so I'll show that, and ask you to use your imagination.

Let us just focus on one of the six sides.  Suppose ROQ is an equilateral triangle, as we had before, so that RQ is one of the six sides of an inscribed hexagon.  We approximated the value of pi by finding the length of RQ (in diameter units) and then multiplying by n = 6.

Our procedure is going to be as follows:  at each step we will halve the angle at P, then compute the new length SQ.  After one cycle, SQ is one side of a 12-sided polygon, so we multiply by 12 to get an approximation for pi.

To carry out this program, we need one more preliminary result.  It is called the angle bisector theorem.  This theorem provides a way to start with the special ratios for any angle, and find the same ratios for one-half that angle.

The line segment b bisects the angle at the left, so the two half-angles labeled theta are equal.  In the upper triangle, we draw the altitude to side c and label it d.  We can do this because the larger of the two triangles formed by the altitude is congruent to the triangle in red with sides a,b,d.  

Next, the small triangle with sides e and d at the top right is similar to the whole starting triangle with sides a,f,c (both are right triangles with one smaller angle gamma).  Similar triangles gives us this ratio:

e/d = c/a

Now add 1 to both sides

e/d + d/d = c/a + a/a

f/d = c/a + a/a

a/d = c/f + a/f

On the right-hand side we have what are called in trigonometry the cosecant and cotangent of the angle 2 theta.  For the case of 2 theta equal to 30 degrees, these are the ratios from above:  c/f = 2 and a/f = square root of 3.  The left-hand side is the cotangent of the half-angle, theta, which is obtained by simple addition.  So the cotangent of 15 degrees is 2 + square root of 3.

Let's just check:

To get the other ratio for the half-angle (b/d), recall that our new triangle has sides a,b,d, and we know the ratio a/d.  But we also know from the Pythagorean theorem that

a^2 + d^2 = b^2 

so

b/d = sqrt(1 + a^2/d^2)

And that's it!  

Going back to this figure

We have that PR/RQ = square root of 3 and PQ/RQ = 2.  We compute the ratios for the half-angle, PS/SQ and PQ/SQ using the method laid out above. 

To get an estimate for pi, invert the last ratio to get SQ/PQ, recall that PQ is equal to 1, and multiply by the number of sides.  We've doubled the number of sides so n = 12. 

The essential code  is:

I set it up as a generator, which is initialized with the values of sine and cosine for 30 degrees.  A gist for the whole program is here.

Here's a screenshot of the results:

The fifth entry gives the result from four doublings as 3.141032.  Archimedes has this estimate in the end as 3-10/71 or about 3.140845.  His lower bound is smaller than ours, because we've used a powerful computer to do very accurate calculations.

One interesting aspect of the whole story is to think about how he may have obtained a rational approximation to the square root of three (all of his calculations were with rational numbers).  That's for another day.

Many thanks to the author of this page and to Neil Carothers.  (His pages have since been disappeared by his university, which hosted them, you may be able to find them by using the wayback machine).  The  post you're reading does things the way Archimedes did them, but there is a simpler formula using the values for the perimeter itself (see my pdf).