Pentagons, again

 It's been some years, but I took another look at pentagons.  It is fun to see the connection between φ,  the "golden ratio", and the internal triangles in a pentagon.

First of all. the figure has five-fold rotational symmetry.

The marked angles in the panel on the left are equal by the isosceles triangle theorem, so the angles on either side of the central angle at each vertex are equal.  

Then we do some addition:  3 black + 2 magenta = 180 = 4 magenta + 1 black.  We conclude that black = mageneta.  So the vertex angle is divided into 3 equal parts.

The small triangle at the top is isosceles, because the triangles on either side are congruent to each other (by rotational symmetry, or ASA), so both sides are equal. Now, we see that the horizontal chord is parallel to the bottom side, by alternate interior angles.  We have a bunch of rhombi!

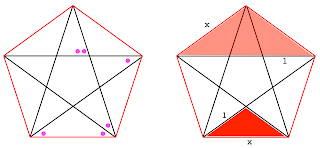
There are two types of similar triangles:  one tall and skinny, the other short and squat.

In the right-hand panel, a triangle of the second type is shown in light red.  It has equal sides of length x and a base of length x + 1.  The red one has sides of length 1 and a base of length x.  We form the equal ratios:  (x+1) /x = x.

One can also use the tall skinny triangles.

This allows the base to have length 1.  Then, the sides of the tall skinny triangle in the middle are x.  The small, tall skinny triangle at the top has sides x - 1 and base x - 2(x - 1) so the ratios of similar triangles are x = (x - 1)/(-x + 2), which simplifies to the same expression as before.

The apex angle of a tall skinny triangle is equal to 1/3 of the interior angle of the pentagon, which is 108/3 = 36.

We will find an expression for the sine of 36°, and this will give us another way to calculate the side length for the pentagon in terms of the chords.

We start by working with 18°, because 90/18 = 5 exactly.  The trick is that (using θ for 18°):  5θ = 90° so 2θ = 90 - 3θ.  Taking the sine of both sides and then converting to the complementary angle on the right, we have sin 2θ = cos 3θ.

One can also use de Moivre's formula and take the real part.

[Since φ - 1 = 1/φ, the above result can be written more simply, but it makes the calculation below more complicated].

There is something else.  If one draws the central angles of the pentagon, then the triangle containing a central angle of 72° and a base of one side length has a half angle of 36°.

So one-half the side length is the sine of 36°, which we found above.  The circle containing the five vertices for a pentagon of side length 1, has a radius of r = 1/2 sin36° = 1/sqrt(3 - φ).

The pdf of the write-up is here (Latex one level down).